
Hydrodynamic Approach to B-O on the Double
Exploiting analyticity condition pertaining to B-O on the double, if we describe the following:

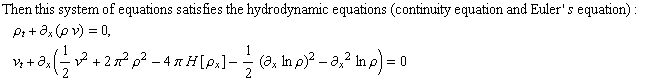
Essentially, then, we have that every solution of B-O on the Double (soliton as well as arbitrary non-soliton solutions)correspond to some description of the hydrodynamic system, and vice-versa.
It is proven that Classical Sutherland Model which describes the interaction of an N-body system with ![]() interaction, in the limit of N going to infinity, turns into continuous hydrodynamic system.
interaction, in the limit of N going to infinity, turns into continuous hydrodynamic system.
We verified this, by taking the actual 1-Soliton Solution of the hydrodynamic system, approximated it with a finite-body Sutherland system, and plotted the evolution of position of the particles, which verified that they travel with a permanent form, just like a Soliton.
The following are the density and velocity functions corresponding to 1-soliton solution in the hydrodynamic representation:
![]()
![]()
Translating it to the Sutherland Model of 100 particles,the initial profile looks like the following:
![[Graphics:HTMLFiles/index_6.gif]](HTMLFiles/index_6.gif)
And it evolves like the following:
Indeed,a Soliton Profile!
| Created by Mathematica (April 26, 2006) |