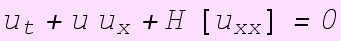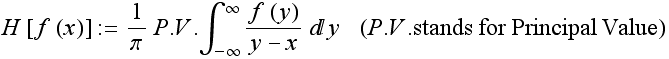UNDER CONSTRUCTION
Benjamin-Ono equations: Solitons and Shock Waves
Abhinav Guliani, Manas Kulkarni
and Alexander Abanov
Stony Brook University

Introducing Solitons
Most Waves in Real-Life do not travel with a permanent profile, that is, dispersion continuously changes the profile of the wave. Since most media are dispersive, they cause waves to change form (disperse). For example, waves on the surface of water. Physicists had long believed that it was impossible to observe such special waves of permanent wave form in any dispersive medium.
In 1834, Sir J.Scott Russel accidentally observed such a wave, that traveled several miles without change of any form, set off by a boat in a canal near Edinburgh. That discovery initiated a series of studies by Russel himself and then by many other physicists who finally confirmed the existence of such waves that are now called Solitons. With advancements in the field of nonlinear analysis, the study of solitons has grown tremendously. They have recently become of great interest to Physicists and Mathematicians due to its observance in many fields such as Optics, Quantum Mechanics, and others.
In mathematical literature, there are many nonlinear equations which are known to have soliton solutions. The Korteweg-deVries Equation, which describes moderately small, shallow-water waves, exhibits Soliton solutions. The Benjamin-Ono equation describes internal waves of deep stratified fluids--it also has Soliton solutions.
Benjamin-Ono Equation
The Benjamin-Ono equation describes internal waves of deep-stratified fluids. It is governed by the following equation, known as the Benjamin-Ono equation:
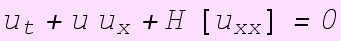
where H is the Hilbert Transform Operator defined by the following:
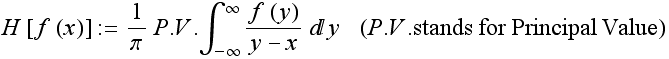
Solitons and Shock Waves