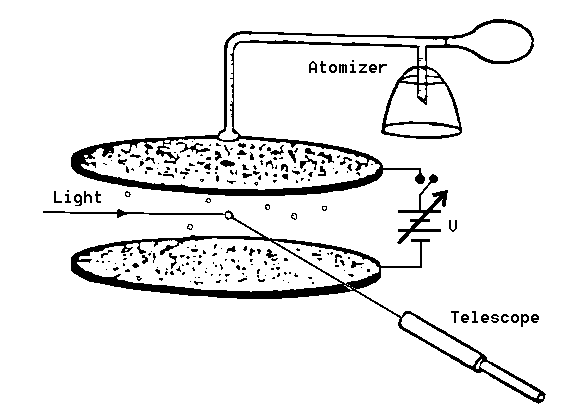
Figure 1: Schematic diagram of Millikan's oil drop apparatus
| PHY 252 | Measurement of the Electron Charge |
The purpose of this experiment is to measure the smallest unit into which electric charge can be divided, that is, the charge of an electron e. The method is the one proposed by R.A. Millikan in 1910. A small sphere of mass m having a charge q can be suspended in air by applying an electric field of field strength E to balance the gravitational force on it. We then have
m g = q E .
We neglect here the (very) small buoyant force. The charge q will in general not be the electron charge but rather an integral multiple of it:
q = n e, with n = 1, 2, 3, ...
When the measurement is repeated several times, e can be found as the largest common denominator of the measured charges q.
In the absence of an electric field, the drops will reach a constant terminal velocity vT after a short time. The viscous force balances the gravitational force, so that the net force acting on the droplet is zero and we have:
m g = K vT ,
where according to Stoke's law:
K = 6p h r ,
with h the viscosity of air (1.83×10-5Nsm-2 at 18°C), r the radius of the spheres (@ 0.50mm). From measuring the terminal velocity vT of free fall, the mass of the spheres can be determined.
Figure 1 shows a schematic sketch of the experimental set-up. A closed chamber is placed between two capacitor plates 0.4 cm apart, in which a uniform electric field E can be built up. The chamber is illuminated by a small lamp. Charged spheres (a suspension of latex in water and alcohol) can be blown into the chamber through a tube and a nozzle, and be viewed there through a telescope with a calibrated scale (spacing of graduations 0.5 mm). Note that the telescope gives an inverted image.

Figure 1: Schematic diagram of Millikan's oil drop apparatus