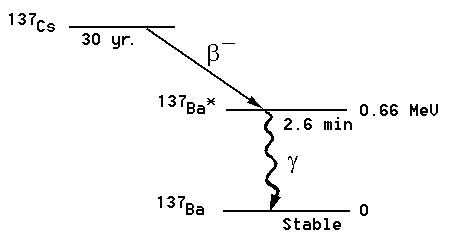
Figure 1: The 137Cs decay chain.
| PHY 252 | Radioactive Decays |
In this experiment we will measure the half-life of an excited state of the 137Ba nucleus. Samples are prepared from a radioactive isotope of 137Cs. This isotope has too many neutrons to be stable; it decays by b-decay into 137Ba*. This daughter nucleus is produced in an excited state, indicated by the asterisk (*). The excited state subsequently decays into the ground state of 137Ba with a half-life of the excited state of 2.6 min. The decay of the excited state is detected by measuring the emitted g-rays of 0.66 MeV. This energy corresponds exactly to the energy difference between the excited state in 137Ba* and the ground state.

Figure 1: The 137Cs decay chain.
The g-ray emission rate R(t) = - dN(t)/dt, where N(t) is the number of 137Ba* nuclei present at time t. The emission rate is proportional to N(t):
dN(t)/dt = -l N(t) ,
where the proportionality factor l is defined as the decay constant. Integration of above expression leads to
N(t) = N0 exp(-lt) ,
where N0 is the number of excited nuclei present at t = 0. The half-life t½ is defined as the time it takes for the activity to be reduced by half; thus, at t = t½, N = N0/2. Derive the relationship between l and t½. Show that at any time t + t½, there will remain only one-half of the excited nuclei that were present at time t !
Correct your data for the background and plot the logarithm of the corrected count rate versus the time t. You should obtain a straight line. Don't forget to put proper errorbars on your data points. From the slope of the straight line you can obtain the half-life and the decay constant (including the errors). Compare with the accepted values.