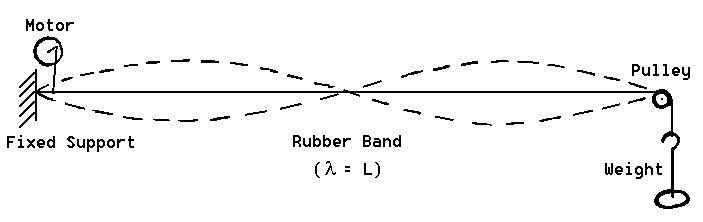
Figure 1: Standing wave (case l = L) on a rubber band.
| PHY 252 | Vibration Spectrum of 1-Dimensional Waves |
In this experiment we study standing waves on a long rubber band stretched between fixed supports. These standing waves are analogous to the wave functions of a particle in an infinitely deep potential well.
If one end of a long rubber band is subjected to forced periodic vibrations, traveling waves will propagate down the rubber band with velocity
| c = Ö(T/m) | (1) |
where T is the tension in the band and m is the mass per unit (stretched) length of the rubber band. The wavelength l is related to the frequency n of the driving force and the velocity of propagation c as l = v/n.
Waves reflecting off the far end of the rubber band interfere with incident waves, and for certain driving frequencies a stable pattern emerges, with fixed points of destructive interference (nodes) and constructive interference (anti-nodes). If the rubber band is very long, the wave is dissipated by friction before it reaches the far end, and no interference occurs. If this is not the case, then the wave can reflect back towards the initial point where it can again be reflected, etc.. For certain wavelengths the reflected wave will be in phase with the next incident wave, resulting in constructive interference. The condition for this to occur is
L = n l/2, with n = 1, 2, 3, ... (integer).
This condition ``quantizes'' the system, so that only certain wavelengths (and thus only certain frequencies) can excite these ``normal modes'' of the system (analogous to eigenvalues in energy).
The rubber band is stretched over a pulley, and the tension T is provided by a weight. A set of scales is provided to be able to measure the weights and the mass of the rubber band, so you can calculate its linear mass density by measuring its total stretched length. (Note: this length will vary with the weight applied!) Start with the rubber band as long as possible (about 2 m). A small electric motor driven by a variable power supply produces the oscillatory driving force near one end of the rubber band. The frequency is measured by a photo-gate and counter.

Figure 1: Standing wave (case l = L) on a
rubber band.