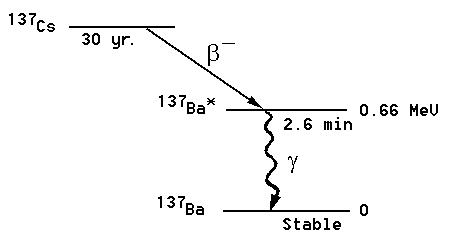
Figure 1: The 137Cs decay chain.
| PHY313/CEI544 | Radioactive Decays |
It happens that in the beta decay of 137Cs, the product (or "daughter") barium nucleus is left in an "excited" state. This decays in a few minutes back to the "ground" state of the barium nucleus, emitting a photon (a quantum of light) of fairly high energy, called a "gamma" ray (technically, gamma rays of energy 0.66 MeV, corresponding to light with wavelength 0.02 Angstroms. The energy of the gamma ray equals the difference between the energy of the excited and ground states of 137Ba.) Such a gamma ray interacts weakly with matter, and will usually penetrate the container and fly into the room where it might be absorbed in your geiger counter detector, especially if you put the sample close to the geiger counter. But don't put it too close -- you might accidentally break the fragile "window" of the counter which will destroy the counter.
Before you begin counting gamma rays from the 137Ba, you should inspect detector, a box, inside which is hidden a Geiger-Müller tube. Adjust the high voltage to a value near 600 V, and then keep it there throughout your measurments. Measure the room "background" for 10 minutes. You will need this information later to correct your counting measurements of 137Ba decays.
We will separate some unstable 137Ba
atoms from the "parent" 137Cs source. This is done by
washing the 137Cs with dilute hydrochloric acid to
dissolve
out the barium. We will give you the resulting solution,
containing
no cesium, only barium.
The technical term for this is "milking
the
cow." The parent 137Cs source is the "cow" and the
solution
we give you is the "milk." The milk contains some excited barium
nuclei which were probably created by very recent decays of the cow
(Cs) atoms.
It also contains some barium atoms in the ground state, which were
probably
created by less recent decays of cow atoms, and have already emitted a
gamma ray and decayed to their ground state. Before too long, the
rest of the barium atoms will also decay into their ground state,
emitting
more gammas, some of which you can measure with your counters.
The
time required for half the "excited" 137Ba nuclei
(these
are designated as 137Ba* nuclei) to decay into ground state
137Ba
nuclei is called the "half-life." This is what I want you to
find out from your measurements.
The answer will probably be a few minutes. You should be able to
measure the half-life to approximately 10% accuracy. This
does
not mean that you are only 90% competent. If you and the group
that
comes after you are both perfectly competent, then the group that comes
after you will probably get an answer 10% smaller or bigger than you
did.
In order to get a more accurate answer, you would have to count many
more
decays.
As soon as Li Li gives you your sample, put it
in the detector, which should be in the "stop" and "reset" mode,
showing zero counts. Then promptly
move the "count" button of your
detector to the "continuous mode" and start timing. At then end
of each minute, record the total counts showing on the detector.
After one half-life has elapsed, only 1/2 of the
137Ba
nuclei remain in the 137Ba* form, and 1/2 will have decayed
to the ground state. After two half-lives have elapsed, only 1/4
of the
137Ba
nuclei will be in the 137Ba* form, and 3/4 will have
decayed
to the ground state. After three half-lives, only 1/8 are 137Ba*.
Therefore,
the
rate of new counts in the counter will be decreasing with
time by corresponding factors. The number of new counts will be
proportional
to the number left in the unstable
137Ba* form. If you
make a graph with the horizontal axis being clock time since you start
counting, and the vertical axis being the total number of accumulated
counts in
your counter since you started counting at time "zero", then the
vertical
axis will show how many 137Ba decays have been detected
plus how many background events have happened. You should then
graph the accumulated number of counts versus time.
How should you
determine the half-life from this graph? I will let you think
about it. For your first try, you can
ignore any correction for background.
When you have finished counting, please give your samples back to Li
Li. Also, please give him a copy of your data (60 sec, # of
counts, 120 sec, # of counts, etc.) Li Li will add the results
of all groups
for each 1 min interval. We will study this additive count graph
either later in the evening or at the next class.

Figure 1: The 137Cs decay chain.
Lab Writeup: