Physics 540 Fall 2005
Homework #3 Due Tuesday Sept. 20

1. Read Bent's essay on Carnot.  Notice the footnote on the bottom of p. 2.  Find a case where Carnot uses the word "caloric" to denote what today we call entropy.
2. The latent heat of fusion of water is 3.34 x 105 J/kg.  The specific heat of water is 4.190 x 103 J/kgK.  The specific heat of ice is about half as much.

a. What is the entropy difference (in J/K) between a mole of water and a mole of ice, both at 273.15 K?
b. Consider a piece of ice in equilibrium with water at 273.15 K.  Suppose one molecule of H2O leaves the ice and joins the water.  What happens to the volume DG(E) of phase space accessible to the system as a result of this event?
c.   What is the difference in entropy between a mole of water and a mole of ice at 263.15 K?  (note: the water is supercooled by 10K below the freezing temperature.  This is actually quite a common event in the atmosphere if there is nothing to nucleate freezing.  We can apply ordinary thermodynamic methods to such metastable states.)
d. The entropy of water exceeds that of ice at 263.15 K.  Why doesn't ice melt at this temperature?  Do not invoke the Helmholtz free energy, just use undergraduate thermodynamics to answer this.
3. Energy in thermodynamics is most directly considered a function of entropy S and V.  In class, the V-dependence was discussed.  See, for example, page 2 of the notes on phase diagrams.  Now consider the S-dependence.  Since dU/dS is T, U is an increasing function of S.   Suppose we have a pure material which can exist in two phases, and we know U(S,V) at some fixed volume V, as shown in the sketch.  Phase 1 might be ice, and phase 2, water.  You have a rigid closed
container (V=const), well insulated thermally from the environment.  You start at low T, adding heat in small increments DQi at temperatures Ti.  The entropy
of the system increases.   The system undergoes a phase change from ice to water.
 
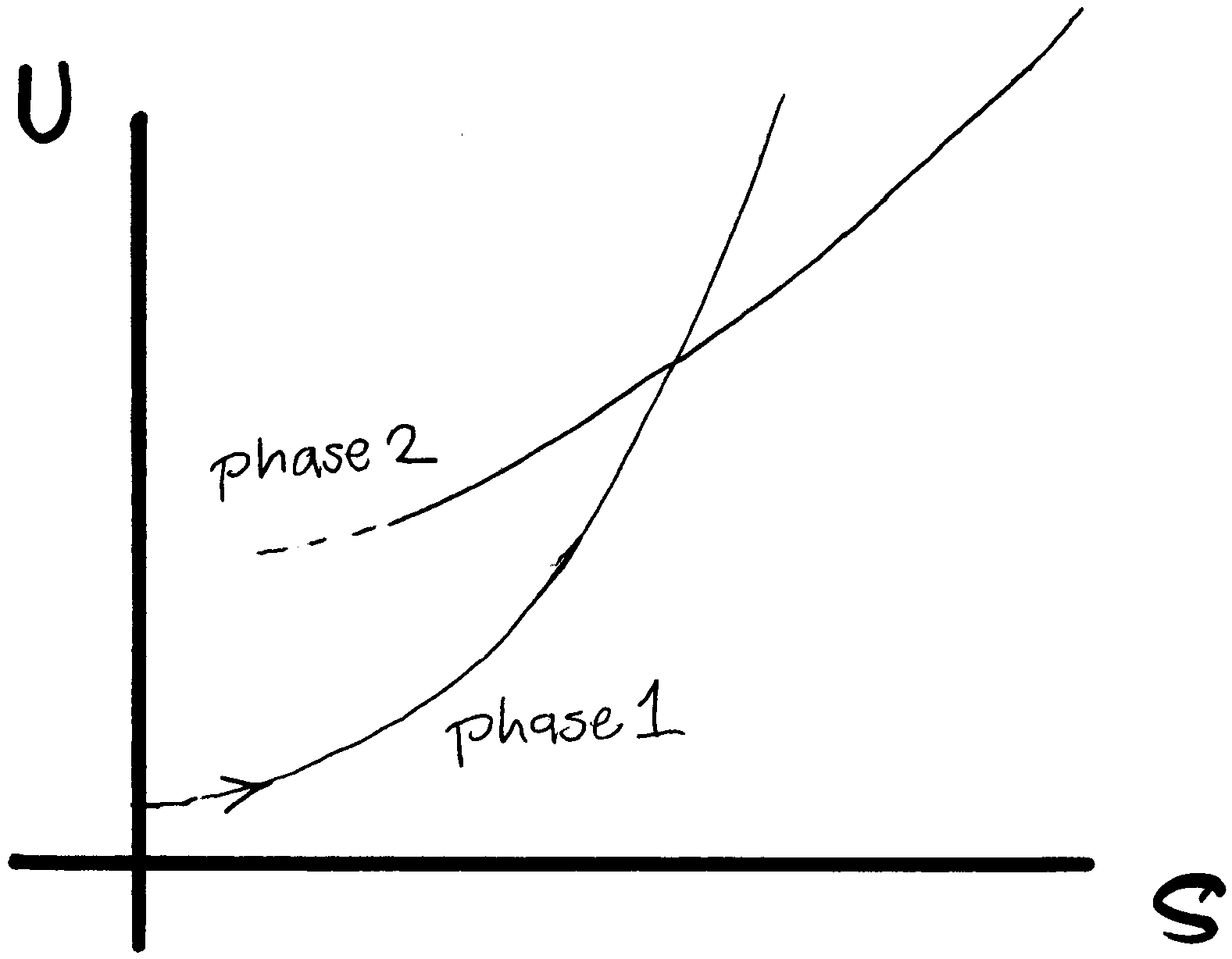a) How do we know that U has uniform upward curvature as a function of S at fixed V?
b) What is the path in the U versus S plane?
c) How would you construct the F versus T graph (at the same fixed V)?  What does the path look like on this graph?
d)  Relate the latent heat to properties of both the U vs S and the F vs T graph.  In particular, try to relate things to S=0 intercepts on the U axis of (a) special line(s).
4. It is often interesting to think about the slope dp/dT of a phase boundary in the P vs T plane.  For example, look at the solid-liquid phase boundary on the P vs T graph for cerium (shown on p. 5 of the notes on phase transitions; the "d-phase" is solid.)  There is a famous relation ("Clausius-Clapeyron equation") relating dp/dT on the phase boundary to the latent heat, temperature, and volume change.  Derive this relation.  You will use the equality of the Gibbs free energy G(p,T) of the two phases on the boundary.  What can you deduce from the apparent divergence of dp/dT and the opposite signs of dp/dT on either side of the
point of divergence?
 

back to Phy540 home page